“VSおとうさん”3年生の算数で勝負
我が家のIntersting Learningの”VSおとうさん”。きょうは、長男が公文の算数で挑みました。3年生の約分です。前回の料理対決の負けを若干引きずっている私ですが、計算問題が得意な長男に一矢報いてもらいたいと思います。
きょうも我が家のヒール(悪役)。いえ、最大の強敵は本気の姿勢を崩さないでしょう。長男は同じく公文に通っている長女、次男と比べて計算問題を解くスピードが一番早いです。宿題もコツコツとするタイプで、計算問題も地道に解いてきました。
”VSおとうさん”とは
子供たち4人と私(妻)が、お父さん(=夫)と対戦します。勝負するテーマは毎回異なります。ルールは簡単。いつもそれっぽく偉そうなこと?を言う夫に挑みます。子どもたちは、勉強(算数、テスト、理科、社会)やスポーツ、遊び、ゲームなどさまざまです。
 強敵(ライバル)おとうさん
強敵(ライバル)おとうさん勝負終了の期間は未定ですが、子供たちとともに「勝ち越したい」という気持ちしかありません。将来的には特別試合(賞品付とか…笑)とかも考えていきたいです。夫のメリットは・・・?子どもたちの時間です。
勝負テーマは「分数の約分」
分数は小学校で習って以降、高校や大学まで使われていたな。ただ、こうやって約分することについて記事を書くとも思っていなかったのでいい機会です。
分数は「分母と分母はそれぞれ素数になるまで約分する」というルールがありましたよね。分母と分子の数を同じ数で割り続けて、小さい数字にしていきますよね。あれ?そもそもなんで約分って必要なんですか?初めて疑問に思いました←ダメじゃんw
分数は同じ数をかけたり割ったりしても値が変わらない
理解しようと調べてみました。ホールケーキを6等分にしたうちの3つ(6分の3)と半分(2等分)したうちの一つ(2分の1)の値は同じということですよね。
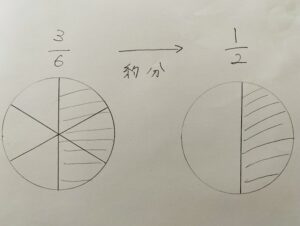
よりシンプルな数字にすることが求められているんですよね。テストの時に見落として減点されたことがあったような気がします。分母と分数の数字を割れる数を見つけていく作業ですが、インターネット上に「なるほど」なアドバイスがありました。
大きい数を見つけようとしない
確かに。割る回数を減らすために大きい数字を見つけようとすると、探す時間にかかってしまいます。2や3など小さい数字で割れば、大きな数字の計算と比べるとミスのリスクも減るでしょうし納得です。
それでは今日も!長男と約分で勝負だ!
勝敗のポイント
①いかに早く解けるか
②正解率
※復習はしっかりしよう
きょうは約分ですので、あっという間に終わります。KUMON(公文HP)で出された宿題の一部で勝負です。間違うポイントとしては約分しきれているか、スピードになってくるでしょう。
今回の問題はあわせて56問を2回に分けて勝負します。一試合28問です。
長男「約分は苦手なんだよな」
父の子か!負けた時の保険をかけたような言葉を発しています。夫はそれに対して無反応です。本気の構えだ。試合前の握手です。

それではスタート!
カリカリカリカリ
カリカリカリカリカリ
カリカリカリカリカリカリカリ
「はい!終わりました」
夫でした……。夫は正答率は100%(当たり前です!笑)長男は、1問約分しきれずに終えていました。またスピードについても2回の勝負ともに夫が数秒早く終えています。しかし、計算が好きな長男はなんとか食らいついていました。惜敗としましょう!

公文式については、また別の記事で紹介したいなと思っていますが、何度も同じ問題を繰り返し繰り返し行うので基礎は付いているなと実感します。また、先々の問題(小2なら小3、小4)を先取りできるので、学校の授業も楽しいようです。
春休みを前にもらった成績表は、あまり良くなかったのはここだけの話です。たくさん遊んで大きくなりましょう。しかし4敗か…次くらいは勝ちたい。
戦績(0勝4敗)






